UNITÉS (SYSTÈMES D’)

UNITÉS (SYSTÈMES D’)

Pour progresser dans la connaissance d’un phénomène quelconque, il faut essayer d’avoir un point de vue quantitatif sur les grandeurs mises en jeu: classiquement, mesurer une grandeur consiste à la comparer à une grandeur de même nature choisie comme unité. Cette opération est parfois très simple: la mesure x d’une longueur l au moyen d’une unité de longueur l ⁰ est telle que l = xl ⁰, l’unité étant bien définie (le mètre, par exemple) ou approximative: «pas d’un marcheur, pied». L’opération de mesure peut cacher un phénomène complexe ou même inconnu: si une substance chimique de formule encore inconnue et n’existant que dans un mélange complexe a été mise en évidence au moyen d’une réaction physiologique chez l’homme ou chez l’animal, l’unité provisoire d’une telle substance pourra être la quantité qui entraîne la réaction physiologique envisagée avec tel critère chez tant d’individus (c’est ainsi qu’une hormone mâle a été mesurée en unités «crête de coq»).

Il y a ainsi deux types d’unités:

1. Les unités qui peuvent se raccorder entre elles par un système cohérent, par exemple l’unité de vitesse, définie par le rapport de l’unité de longueur à l’unité de temps.

2. Les unités définies spécialement pour un phénomène. Dans ce second groupe, on distingue encore deux cas:

– La définition de ces unités cache une méconnaissance, qui peut n’être que provisoire, des phénomènes: par exemple, après purification et expérimentation, l’unité «crête de coq» pourra correspondre à y microgrammes d’un composé chimique défini Y; néanmoins, par habitude ou par commodité, une telle unité subsiste parfois longtemps après que le phénomène correspondant a été éclairci; ainsi, on a d’abord défini l’unité de radioactivité, le curie (activité d’une source d’environ 1 g de radium), pour effectuer des comparaisons; bien que l’on ait ensuite adopté une autre unité, le becquerel (symbole: Bq; activité d’une quantité de nucléide radioactif pour laquelle le nombre moyen de transitions nucléaires spontanées par seconde est égal à 1), l’usage du curie (symbole: Ci) a été toléré jusqu’au 31 décembre 1985 (1 Ci = 3,7 憐 10¹⁰ Bq).

– L’introduction d’unités définies spécialement pour un phénomène ou une grandeur peut cacher une méconnaissance qui risque d’être éternelle: par exemple, on «mesure» le coefficient intellectuel d’un individu. Il ne faut pas rejeter a priori une «mesure» de ce type: toute tentative de mesure oblige à réfléchir et entraîne une augmentation des connaissances; d’autre part, il est bon de pouvoir comparer plusieurs individus. Mais il ne faut surtout pas attribuer un sens trop précis à cette «mesure» (à sa connaissance, le coefficient intellectuel de l’auteur n’a jamais été mesuré et, par conséquent, il n’a ni à se justifier d’une mesure qu’il trouve trop faible, ni à faire appel à sa modestie pour corriger une mesure jugée trop élevée).

On va maintenant voir comment on peut imaginer des unités formant entre elles un système logique en mécanique, en électromagnétisme, en photométrie et en thermométrie.

Mécanique

Dans le cadre de la mécanique, on envisagera l’étude de la géométrie, de la cinématique et de la dynamique.

Géométrie

Longueur

Quant l’unité de longueur l ⁰ est définie, la mesure x de la longueur l est telle que l = xl ⁰.

Surface

En abordant les mesures de surface, on peut montrer, en comparant trois rectangles 1, 2 et 3 dont les côtés l et l sont respectivement l ¹ et l ¹ , l ² = l ¹ et l ² = l ³ , l ³ et l ³ , que les surfaces correspondantes S¹, S² et S³ sont telles que:

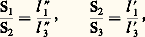ce qui entraîne:

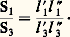La surface d’un rectangle i s’exprime donc sous la forme Sⁱ = kl ⁱ l ⁱ , la constante k étant universelle. Dans les mêmes conditions, la surface d’un cercle de rayon R est S = k 神R². L’unité de surface s ⁰ a été choisie comme égale à la surface d’un carré dont l’arête est égale à l’unité de longueur l ⁰; par définition, on a s ⁰ = kl ²⁰; il vient par conséquent:

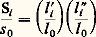pour le rectangle et:

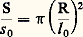pour le cercle. Bien d’autres choix sont évidemment possibles: on aurait pu décider que l’unité de surface correspondît à la surface d’un cercle de rayon unité, et, dans ces conditions, s ⁰ size=1^神 = k 神l ²⁰; dans ce système, on aurait:

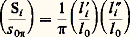pour le rectangle et:

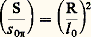pour le cercle. Il est important de remarquer qu’un changement de la définition d’une unité permet de faire apparaître ou disparaître dans telle ou telle expression une constante universelle, ici 神 (cf. Électricité et magnétisme et Rationalisation et non-rationalisation, et ÉLECTRICITÉ - Electromagnétisme, chap. 5). Il est encore possible de définir une unité de surface sans aucun lien logique avec les unités de longueur: en pays de vignobles, on exprime bien encore les superficies en «journée» (superficie de vigne qu’un ouvrier peut vendanger en une journée); mais aucun système «officiel», fût-il anglo-saxon, n’a utilisé cette possibilité d’échapper à la cohérence.

Volume

Des considérations analogues à celles que l’on vient de développer au sujet des surfaces peuvent être effectuées sur les volumes. L’unité de volume v ⁰ a été choisie comme égale au volume d’un cube dont l’arête est égale à l’unité de longueur; dans ces conditions, le volume d’un parallélépipède rectangle de côté Lⁱ , Lⁱ et Lⁱ t est:

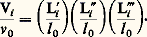Angle (sous-entendu: angle plan)

L’angle compris entre deux demi-droites issues du même point est proportionnel (facteur 見) au rapport de la longueur l de l’arc découpé sur la circonférence d’un cercle (ayant son centre en ce point) à celle du rayon R du cercle = 見l /R; si le radian est choisi comme unité d’angle, on a:

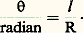Angle solide

L’angle solide d’un cône est proportionnel (facteur 廓) au rapport de l’aire S découpée par ce cône sur une surface sphérique (ayant son centre au sommet de ce cône) au carré du rayon de la sphère 行 = 廓S/R²; si le stéradian est choisi comme unité d’angle solide, on a:

En résumé, toutes les mesures de géométrie peuvent être effectuées de façon cohérente après avoir choisi une seule unité fondamentale: l’unité de longueur .

Cinématique

Temps

Quand l’unité de temps t ⁰ est définie, la mesure y d’un temps t est telle que t = yt ⁰.

Fréquence

La fréquence d’un phénomène périodique est le rapport d N/d T du nombre de périodes d N observées pendant le temps d T.

Vitesse

La vitesse d’un mobile est définie par: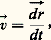

où る est le vecteur définissant, à partir d’un point considéré comme origine, la position du mobile. Quand le mobile se déplace sur une droite (ou que l’on considère la projection de la vitesse sur cette droite), on a simplement:

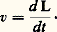Si l’unité de vitesse v⁰ est la vitesse d’un mobile se déplaçant uniformément de l’unité de longueur l ⁰ pendant l’unité de temps t ⁰, on a:

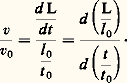Accélération

L’accélération ゔ d’un mobile est définie par:

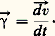Quand l’unité d’accélération 塚⁰ est l’accélération d’un mobile en mouvement uniformément accéléré dont la vitesse varie de l’unité de vitesse v⁰ pendant l’unité de temps t ⁰, on a:

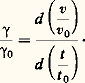Dynamique

La loi fondamentale de la dynamique établit une relation entre deux grandeurs que l’on n’a pas encore rencontrées: la masse m et la force づ; en effet, dans un repère galiléen, la force づ agissant sur un mobile de masse m est égale à la dérivée temporelle de la quantité de mouvement m :

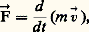et, plus simplement, pour un mobile de masse constante, on a:

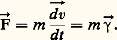Il est évidemment possible de définir arbitrairement les unités de masse et de force; mais, si l’on veut édifier un système cohérent d’unités, un seul choix arbitraire est possible puisqu’il existe un lien entre ces deux grandeurs. Traditionnellement, c’est l’unité de masse qui est déterminée de façon arbitraire.

Masse

Quand l’unité de masse m ⁰ a été choisie, la mesure z d’une masse m est telle que m = zm ⁰.

Force

L’unité de force ⁰ est la force qui s’exerce sur un mobile de masse unité quand il est soumis à l’unité d’accélération; dans ces conditions, on a:

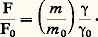Travail et énergie

Le travail d’une force づ, ou l’énergie qu’elle fournit quand son point d’application se déplace de d L 轢, est:

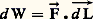Il y a donc intérêt à définir l’unité d’énergie comme le travail fourni par la force unité ⁰ quand son point d’application se déplace de la longueur unité.

Puissance

La puissance étant définie par:

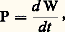l’unité de puissance P⁰ sera la puissance d’une source fournissant uniformément au cours du temps une unité d’énergie pendant l’unité de temps.

Les unités nécessaires pour l’ensemble de la géométrie, de la cinématique et de la mécanique peuvent ainsi être déterminées de façon cohérente à partir de trois unités de base relatives à la longueur, à la masse et au temps. Le système international (S.I.) est fondé sur le mètre, le kilogramme et la seconde (système M.K.S.). Les définitions actuelles du mètre, du kilogramme et de la seconde sont données dans le chapitre sur les unités de base. Son seul concurrent a été le système C.G.S. (centimètre, gramme, seconde). Le tableau 1 donne la liste des grandeurs dont les unités ont reçu des noms spéciaux.

Électricité et magnétisme

La définition des unités dans le domaine de l’électromagnétisme est une question très débattue et sur laquelle un accord unanime des physiciens n’a pu être dégagé. Pour suivre avec profit l’exposé des difficultés correspondantes, le lecteur est prié de se reporter à l’article ÉLECTRICITÉ - Electromagnétisme. Tous les physiciens sont d’accord pour calculer les forces d’interaction dans le vide, soit entre deux charges électriques Q et Q , soit entre deux circuits parcourus par des courants I et I , à partir des lois élémentaires de Coulomb et de Biot-Savart-Laplace:

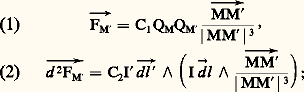la discussion porte sur la nature (nombre ou grandeur) des constantes C¹ et C².

Nature des constantes C¹ et C²

L’étude de l’électromagnétisme montre que ces constantes sont toujours liées par la relation C¹ = C²c ², où c est la vitesse de la lumière dans le vide. On peut arbitrairement dire que l’une de ces constantes est un nombre, mais la nature de l’autre est ainsi déterminée; on arrive à deux descriptions dissymétriques possibles: l’option électrostatique , pour laquelle C¹ est un nombre et C² un nombre divisé par c ², et l’option magnétostatique pour laquelle C² est un nombre et C¹ un nombre multiplié par c ².

Il existe deux présentations symétriques: la première consiste à dire que ni C¹ ni C² ne sont des nombres mais des grandeurs; la seconde abandonne la définition la plus usuelle de l’intensité d’un courant électrique (I = d Q/dt , rapport d’une charge à un temps, seule définition utilisée par les techniciens) pour la remplacer par une autre (attention à l’indice G!):

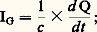dans ces conditions, quand, dans l’expression de la force (2), on remplace I par I^G, il faut corrélativement changer C² en C^2G (avec C^2G = C²c ²); les constantes C¹ et C^2G sont donc identiques (C¹ = C²c ²) et peuvent être égales au même nombre.

Rationalisation et non-rationalisation

Outre la nature de C¹ et de C², il existe un autre arbitraire dans les équations de l’électromagnétisme, arbitraire lié aux places où apparaissent certains facteurs «4 神» dans les équations de base. La rationalisation est l’opération qui consiste à faire disparaître le facteur 4 神 (cf. Mécanique , sous le sous-titre Géométrie, la discussion sur l’apparition ou la disparition du facteur 神 dans les expressions des surfaces) des équations que l’on considère comme fondamentales, c’est-à-dire les équations de Maxwell (cf. ÉLECTRICITÉ - Électromagnétisme, chap. 5).

Les différents systèmes

Les différents points de vue signalés ci-dessus (nature de C¹ et de C², rationalisation) peuvent se combiner de façon indépendante; mais, pratiquement, il n’existe que quatre systèmes à examiner. Pour chacun, on indique sur le tableau 2 la forme des équations de Maxwell, les relations entre les inductions et les champs, les valeurs de C¹ et de C².

Ces différentes expressions sont indépendantes des unités choisies; mais, néanmoins, les trois premiers systèmes sont toujours utilisés en partant du système C.G.S., tandis que le dernier système est toujours couplé au système M.K.S. pour former le système international (S.I.) défini par le mètre, le kilogramme, la seconde et l’ampère (M.K.S.A.).

Dans les trois premiers systèmes, la considération des relations (1) et (2) permet d’introduire de façon cohérente toutes les unités électromagnétiques à partir des unités mécaniques. Pour le dernier système, au contraire (C¹ et C² sont des grandeurs et non des nombres), la relation (2), qui introduit deux grandeurs nouvelles (C² et I), permet de définir de façon arbitraire une nouvelle unité (cf. discussion précédente sur づ = m ゔ); c’est l’unité d’intensité de courant qui a été choisie comme unité de base; cette unité (ampère) a été définie comme égale au dixième de l’unité d’intensité de courant du système C.G.S. électromagnétique, ce qui impose, tous calculs effectués, que l’on ait C² = 10^-7 unité M.K.S.A., d’où la valeur de la perméabilité magnétique du vide 猪⁰ = 4 神 憐 10^-7 H.m^-1. Le tableau 3 fournit les principales unités électromagnétiques dans les différents systèmes: seul le système S.I. est le système résultant des délibérations du Bureau international des poids et mesures (B.I.P.M.). N’y figurent que les grandeurs dont les unités ont reçu un nom particulier; les autres unités s’obtiennent par combinaison: le champ électrique s’évalue en volts par mètre, la densité de courant en ampères par mètre carré, etc.

Photométrie

Le flux lumineux F d’un rayonnement monochromatique de longueur d’onde s’obtient en multipliant le flux d’énergie 淋 correspondant (évalué en watts dans le système M.K.S.) par un facteur K() d’efficacité lumineuse (cf. PHOTOMÉTRIE, chap. 1). Ces facteurs, définis en 1924 et en 1933 par des organismes internationaux, sont relatifs à la sensibilité d’un œil humain moyen. Pour un rayonnement non monochromatique, on a:

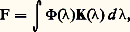淋()d étant la puissance de ce rayonnement transmise entre et + d.

L’intensité lumineuse I d’une source ponctuelle dans une direction est le rapport:

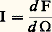du flux élémentaire d F émis par la source à l’intérieur d’un élément d’angle solide d 行 centré sur la direction à l’étendue de cet angle solide d 行.

L’éclairement lumineux E d’une surface est la densité superficielle:

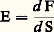du flux lumineux reçu par cette surface. Le flux lumineux total reçu par la surface est donc:

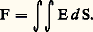L’unité d’intensité lumineuse est considérée comme une unité de base. Dans ces conditions, l’unité de flux lumineux est égale au produit de l’unité d’intensité lumineuse par 1 stéradian, tandis que l’unité d’éclairement est égale au rapport de l’unité de flux lumineux à l’unité de surface.

Le tableau 4 représente les unités photométriques qui ont reçu un nom dans les systèmes S.I. et C.G.S.: les autres unités s’obtiennent par combinaison; ainsi la luminance se mesure en candela par mètre carré (cd.m^-2).

Thermométrie

Toutes les unités thermométriques se définissent à partir des mesures de températures et des unités déjà évoquées. L’unité de température est une unité de base.

Unités de base du système international (ou S.I.)

Les définitions des unités de base sont données ci-dessous, avec leur date d’adoption par la Conférence générale des poids et mesures.

Mètre. Le mètre est la longueur du trajet parcouru dans le vide par la lumière pendant une durée de 1/299 792 458 seconde (1983).

Kilogramme. Le kilogramme est égal à la masse du prototype international du kilogramme (1901).

Seconde. La seconde est la durée de 9 192 631 770 périodes de la radiation correspondant à la transition entre les deux niveaux hyperfins de l’état fondamental de l’atome de césium 133 (1967).

Ampère. L’ampère est l’intensité d’un courant électrique constant qui, maintenu dans deux conducteurs parallèles, rectilignes, de longueur infinie, de section circulaire négligeable et placés à une distance de 1 mètre l’un de l’autre dans le vide, produirait entre ces conducteurs une force égale à 2 憐 10^-7 newton par mètre de longueur (1948).

Unité de température. Le kelvin (K) est la fraction 1/273,16 de la température thermodynamique du point triple de l’eau (1967); le degré Celsius (⁰C) est égal au kelvin.

Unité d’intensité lumineuse. La candela (cd) est l’intensité lumineuse, dans une direction donnée, d’une source qui émet un rayonnement monochromatique de fréquence 540 憐 10¹² hertz et dont l’intensité énergétique dans cette direction est 1/683 watt par stéradian (1979).

Unité de quantité de matière. La mole (mol) est la quantité de matière d’un système contenant autant d’entités élémentaires qu’il y a d’atomes dans 0,012 kg de carbone 12 (1971).

On trouvera dans le tableau 5 les noms et les symboles des préfixes servant à former les multiples et sous-multiples décimaux des unités S.I.

Encyclopédie Universelle. 2012.